First Summer 2019 Meeting
In our first meeting of the summer, we enjoyed a lecture from Professor Chris Rogan about statistics in the context of machine learning.
Margaret started off the meeting with a brief introduction on the purpose of Learning Machine Learning, what the club did last semester and what we plan to do this summer. In the coming weeks we will focus primarily on paper discussions of various aspects and applications of machine learning in different subfields of physics. We will also have a couple of tutorials this summer. For a complete list of weekly events, updated with meeting minutes, see our Schedules page.
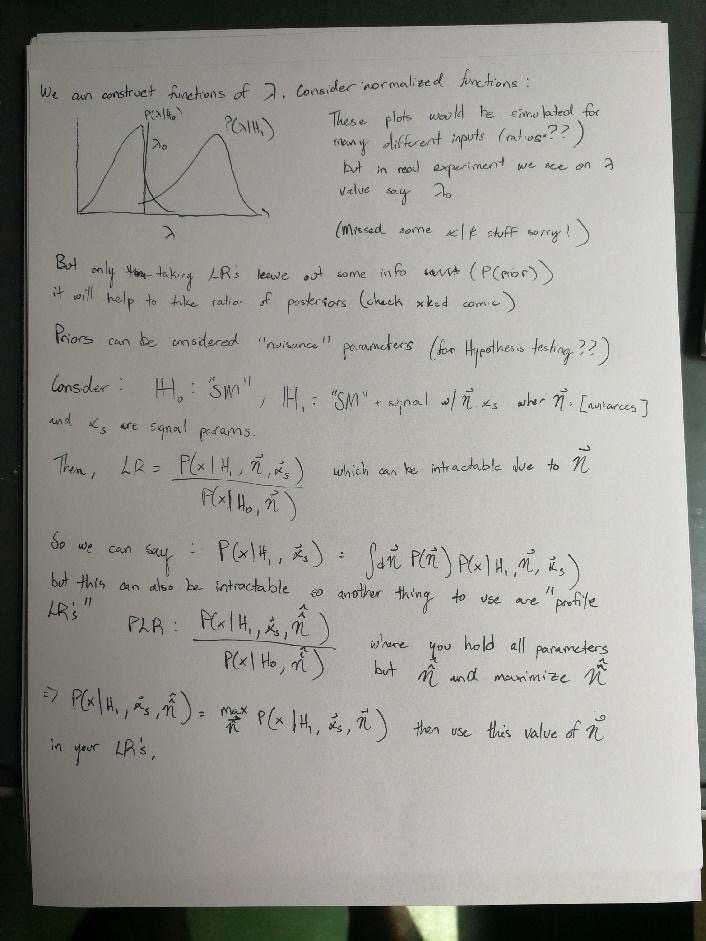
Professor Rogan began his lecture on statistics by examining discrete and continuous probabilities. He also emphasized the sum and product rules as fundamental rules of statistics. From the product rule, we can derive Bayes’ theorem. In the context of Bayes’ theorem, we discussed the differences between inductive and deductive reasoning. We also examined the components of Bayes’ theorem: P(A|B) = (P(B|A)P(A)) ⁄ (P(B)). P(A|B), or the probability of event A given event B, is the posterior. P(A) is the prior, or how much we believe event A will happen. P(B|A), the probability of event B given event A is the likelihood. The denominator of Bayes’ theorem, P(B), can be thought of as a normalization factor.

After examining Bayes’ theorem, Professor Rogan discussed hypothesis testing. Given two hypotheses, H0, or the null hypothesis, and H1, the alternative hypothesis, we can quantify our confidence in one hypothesis over the other based on our data. This is done with the p-value, alpha-value, and beta-value. We also discussed the Neyman-Pearson lemma, how the ratio of likelihoods of the two hypotheses is the universally most powerful value to distinguish between the two.

To wrap up, we took a peek at how machine learning algorithms try to approximate this likelihood ratio. Next week we will dive into machine learning algorithms, their terminology and how they work.
Notes